インボリュート歯車について

2軸が平行な歯車の設計において、回転を伝達する2つの歯車の角速度$\omega_1$,$\omega_2$の比、すなわち角速度比$u$は速比とも呼ばれ、2つの歯車の接触点から各歯車の回転軸までの長さ$r_1$,$r_2$の比に反比例する。このとき角速度比$u$は、次の式で表される。

$$ u=\frac{\omega_1}{\omega_2}=\frac{r_1}{r_2} $$

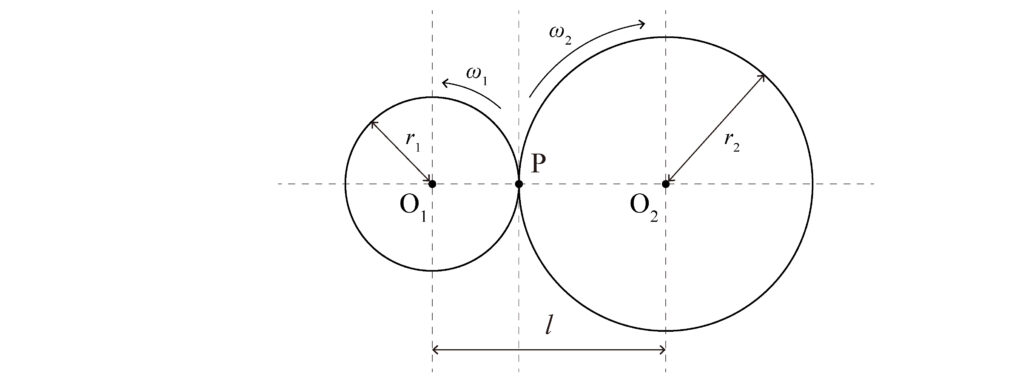
この比が常に一定であるためには、上図(Fig.1)に示すように、２つの歯車の歯の接触点における共通法線が常に回転中心を連結する線上の定点を通る必要がある。

この条件を満たすために標準的な工業用歯車の歯形曲線は、インボリュート曲線(involute)となっている。ここでは、インボリュート曲線についての説明と歯車に用いる上での特徴について整理する。

インボリュート曲線とは？
1. インボリュート関数
2. インボリュート曲線の媒介変数表示
インボリュート歯形の特徴
1. 圧力角
2. 角速度比

インボリュート曲線とは？

伸開線とも呼ばれ、基準となる円(基礎円: base circle)に巻き付けた糸をたるまないように外して行った際に糸の先端が描く軌跡。この曲線の特徴として、円からインボリュート曲線までの接線の長さと、接点までの円弧の長さが等しくなる。

インボリュート関数

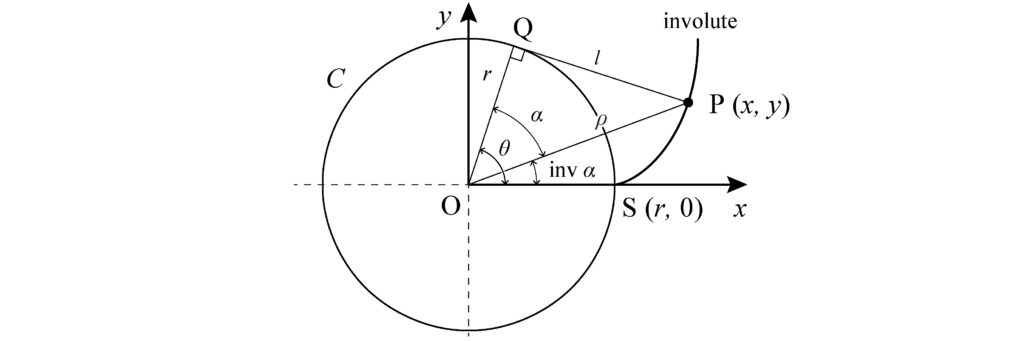
上図(Fig.2)のように、半径$r$の円$C$の中心$O$を原点とするxy軸を設定し、座標$ (r$, 0$)$を点$S$とする。点$S$を始点とするインボリュート曲線上の点を$P$、点$P$を通る円の接線の円との接点を$Q$とする。$\angle POS$はインボリュート関数(involute function) $\text{inv} \alpha$[rad]と定義する。$\angle POQ$を$\alpha$[rad]としたとき、インボリュート曲線の定義より接線$PQ$の長さ$l$と円弧$\stackrel{\frown}{SQ}$の長さは等しくなるため、以下の式で表せる。

$$ l = r\tan\alpha = \stackrel{\frown} {SQ} = r\theta $$

よって、$\tan\alpha = \theta $ であり、

$$ \text{inv} \alpha = \theta -\alpha = \tan\alpha -\alpha $$

である。

インボリュート曲線の媒介変数表示

点$P$の座標($x$, $y$)を媒介変数表示すると、

$$ x=\rho\cos(\text{inv}\alpha) $$

$$ y=\rho\sin(\text{inv}\alpha) $$

であり、原点$O$から点$P$までの距離$\rho$は、$\displaystyle \rho = \frac{r}{\cos\alpha}$で表されるため、

$$ x=r\frac{\cos(\text{inv}\alpha)}{\cos\alpha} = r\frac{\cos(\theta -\alpha)}{\cos\alpha}$$

$$ y=r\frac{\sin(\text{inv}\alpha)}{\cos\alpha} = r\frac{\sin(\theta -\alpha)}{\cos\alpha}$$

ここで、余弦および正弦の加法定理より、

$$\cos(\theta -\alpha)=\cos\theta \cos\alpha +\sin\theta\sin\alpha$$

$$\sin(\theta -\alpha)=\sin\theta \cos\alpha -\cos\theta\sin\alpha$$

であるから、$\theta$を用いて点$P$の座標($x(\theta)$, $y(\theta)$)を媒介変数表示すると、

$$ x(\theta)= r\frac{\cos(\theta -\alpha)}{\cos\alpha}= r(\cos\theta+\theta \cos\theta)$$

$$ y(\theta)= r\frac{\sin(\theta -\alpha)}{\cos\alpha}= r(\sin\theta-\theta\cos\theta)$$

基礎円の半径を1としたとき、インボリュート関数$\text{inv}\alpha$を$[0,\pi]$の範囲でアニメーションを用いてインボリュート曲線を示すと以下(Fig.3)のようになる。

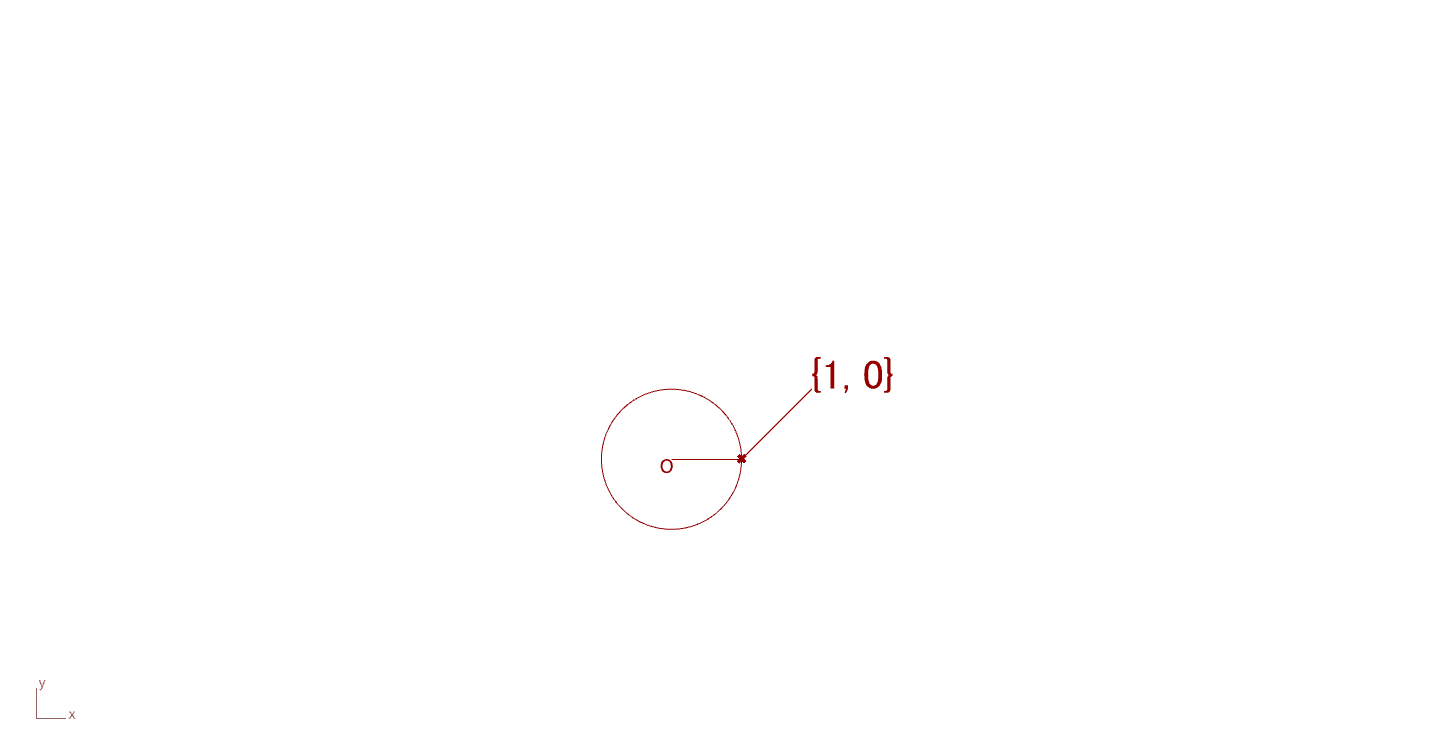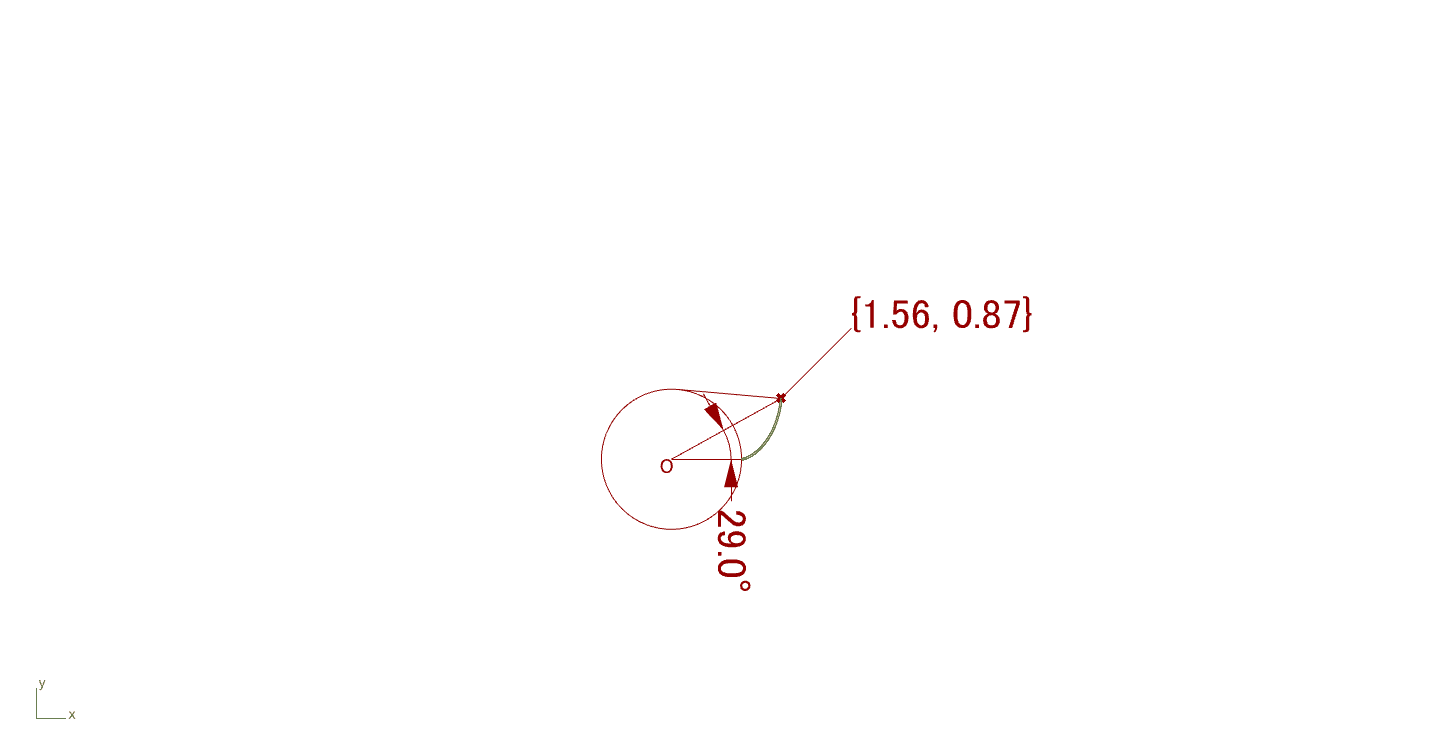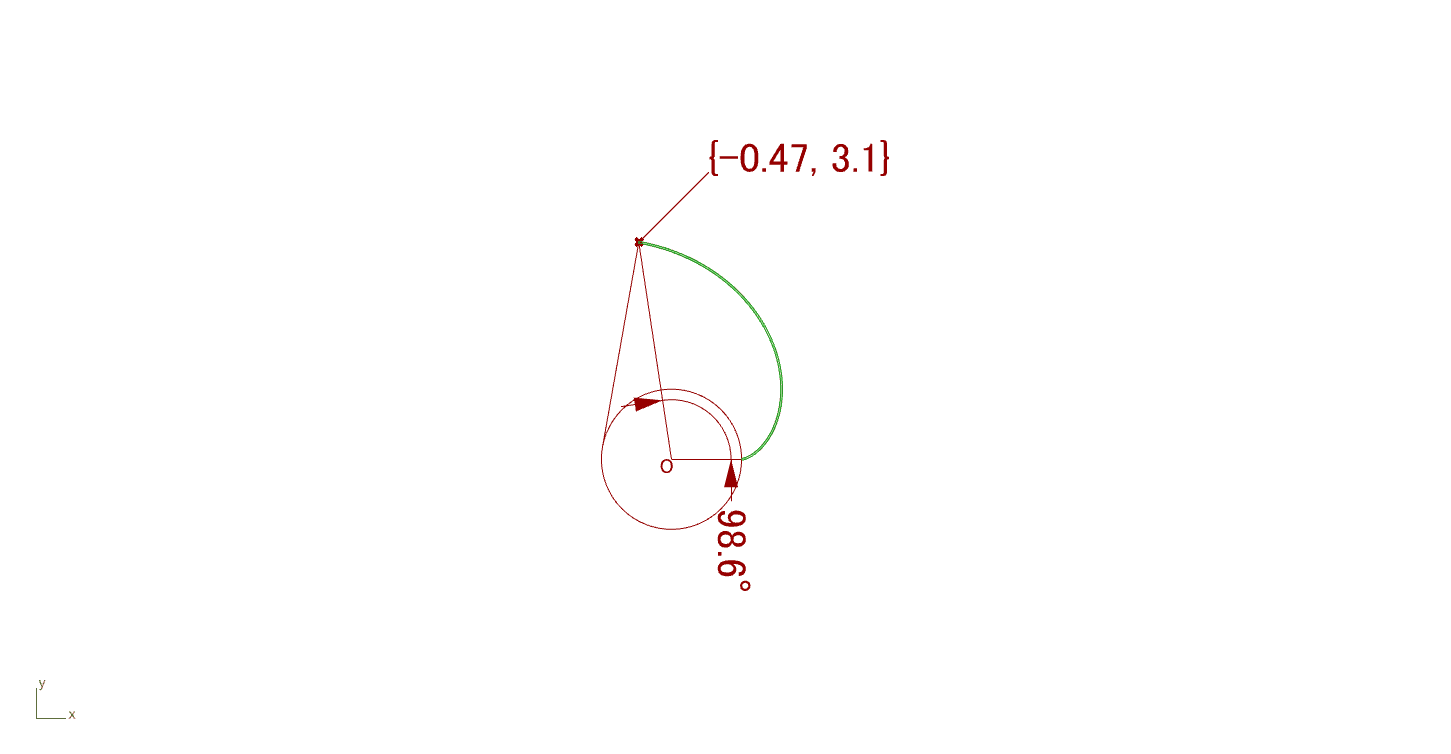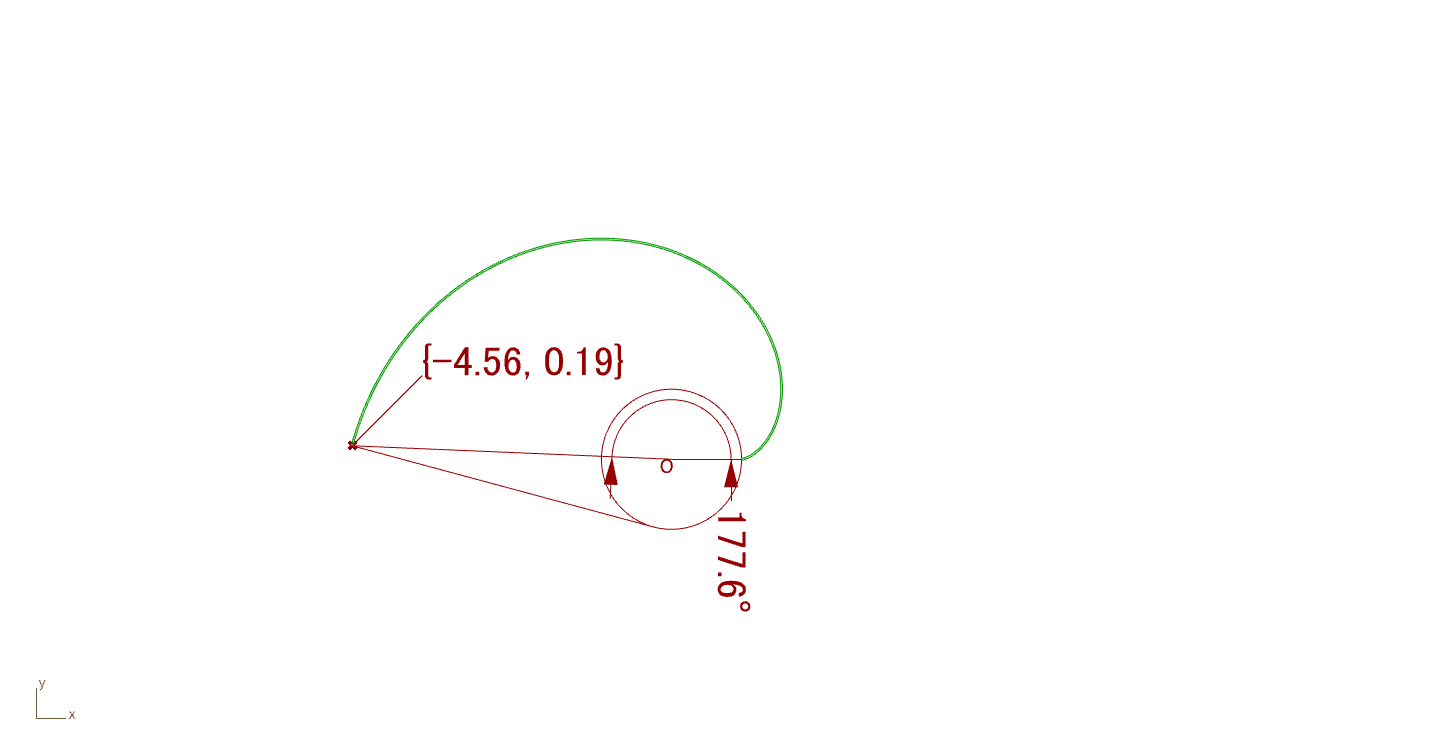
インボリュート歯形の特徴

圧力角

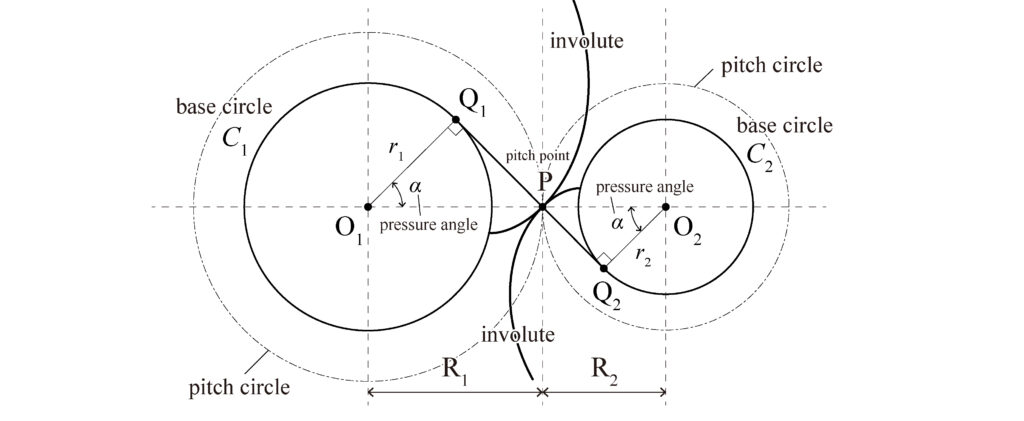
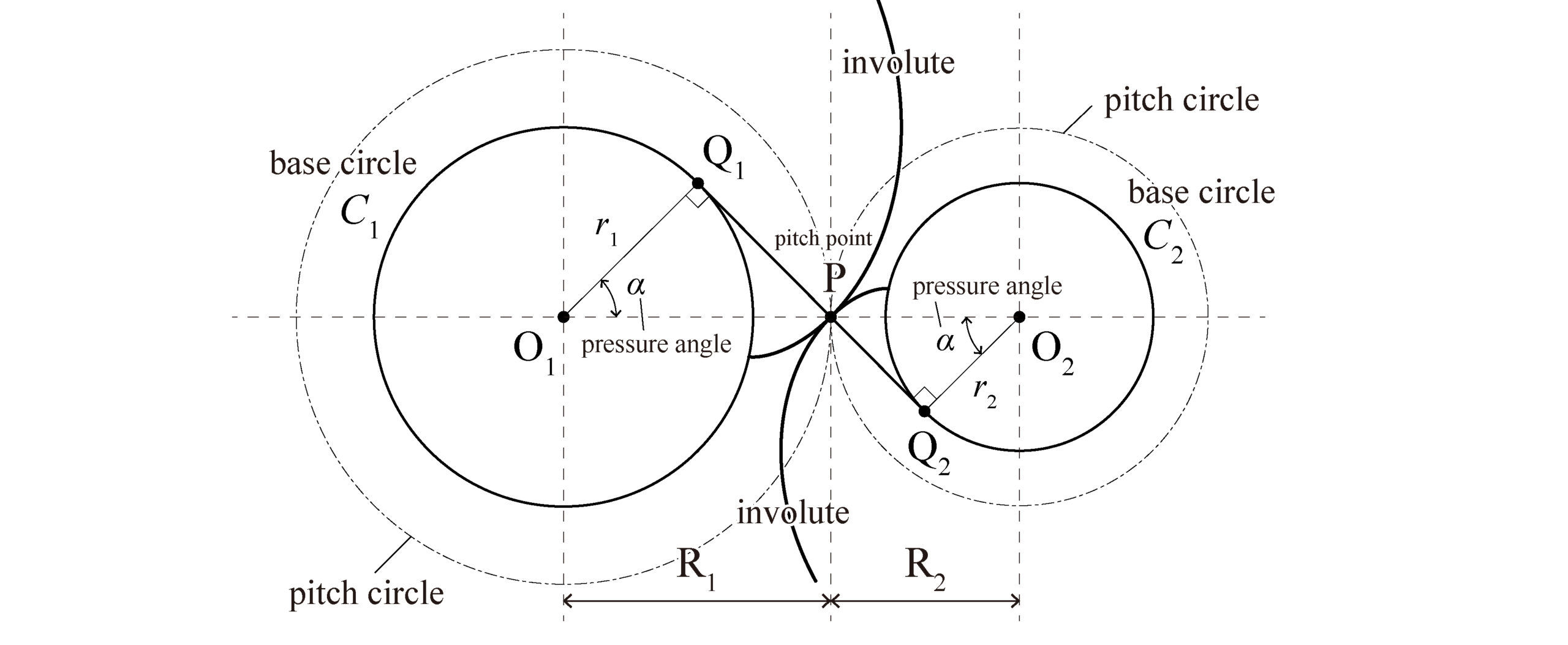
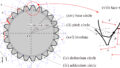
上図(Fig.4)のように、２つの基礎円にそれぞれインボリュート曲線を用いて回転を伝達させたい場合、２つの基礎円への共通接線$Q_1,Q_2$がインボリュート曲線の共通法線となる。つまり、インボリュート曲線の接触点$P$(ピッチ点: pitch point)は常にこの法線上となり、$O_1P$と$O_2P$がそれぞれの歯車のピッチ円の半径$R_1,R_2$となる。

このときの接触点の軌跡は$O_1Q_1$と$O_2Q_2$を半径とするそれぞれの基礎円の共通接線$Q_1Q_2$上に描かれ、接触点の軌跡と点$P$を通るピッチ円の共通接線とのなす角$\alpha$を圧力角(pressure angle)と呼ぶ。そして、インボリュート歯形同士が噛み合っているときの圧力角$\alpha$は常に一定になるという特徴がある。

一般的には圧力角$\alpha$は$20^\circ$が標準とされている。

角速度比

Fig.3より、$\angle Q_1O_1P=\angle Q_2O_2P=\alpha$ であり、

$$r_1=R_1\cos\alpha,\quad r_2=R_2\cos{\alpha}$$

であるから、角速度比$u$は、

$$u=\frac{\omega_2}{\omega_1}=\frac{R_1}{R_2}=\frac{r_1}{r_2}$$

となる。このようにピッチ点までの中心距離$R_1,R_2$が変化しても基礎円の半径の比が変わらない限り角速度比が変わらないことがインボリュート歯形の長所である。

また、２つの歯車の回転数比は歯数をそれぞれ$z_1$,$z_2$、ピッチ円上で測ったときの隣接歯の距離(円ピッチ: circular pitch)を$t$とすると、

$$ z_1=\frac{2\pi r_1}{t}, z_2=\frac{2\pi r_2}{t} $$

であり、$\displaystyle \frac{r_1}{r_2}=\frac{z_1}{z_2} $ より、$\displaystyle u=\frac{z_1}{z_2}$ となる。