In the design of gears with two parallel axes, the ratio of the angular velocities \(\omega_1\) and \(\omega_2\) of the two gears transmitting rotation, or angular velocity ratio \(u\), also called velocity ratio, is inversely proportional to the ratio of the lengths \(r_1\) and \(r_2\) from the contact point of the two gears to the axis of rotation of each gear. The angular velocity ratio \(u\) is then expressed by the following equation.
$$ u=\frac{\omega_1}{\omega_2}=\frac{r_1}{r_2} $$
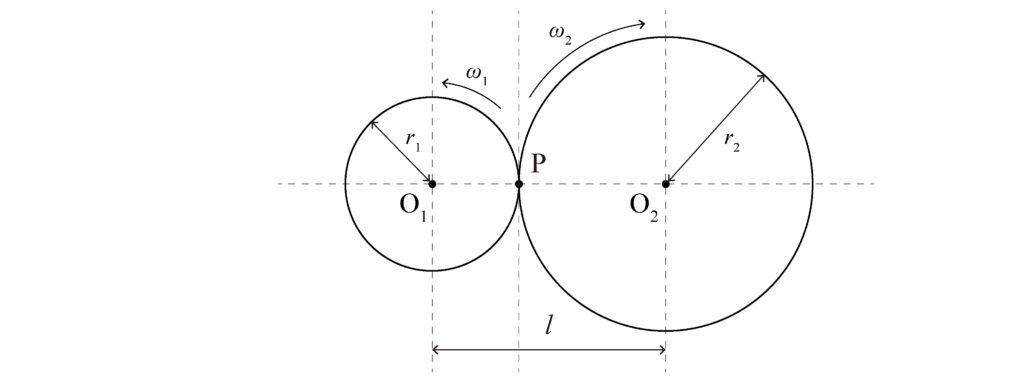
For this ratio to always be constant, the common normal at the contact point of the two gear teeth must always pass through a fixed point on the line connecting the centers of rotation, as shown in the figure above (Fig. 1).
To satisfy this requirement, the standard industrial gear tooth profile curve is an involute curve. Here, the involute curve is explained and its features for use in gears are summarized.
What is an involute curve?
Also called a stretch line, this is the path drawn by the tip of a thread when it is wound around a reference circle (base circle) and removed so that it does not sag. The characteristic of this curve is that the length of the tangent line from the circle to the involute curve and the length of the arc to the tangent point are equal.
involute function
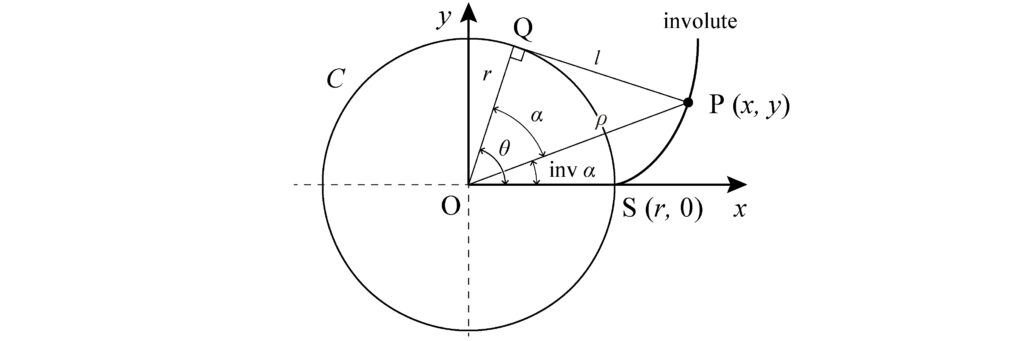
As shown in the above figure (Fig. 2), set the xy-axis with the origin at the center \(O\) of the circle \(C\) of radius \(r\) and the coordinates ( \(r\), \(0\)) as point \(S\). Let \(P\) be a point on the involute curve starting at point \(S\) and \(Q\) be the tangent point to the circle of the tangent line of the circle passing through point \(P\). \(\angle POS\) is defined as the involute function \(\text{inv} \alpha\)[rad]. When \(\angle POQ\) is \(\alpha\)[rad], the length of tangent line \(PQ\) \(l\) and arc \(\stackrel{\frown}{SQ}\) are equal from the definition of involute curve.
$$ l = r\tan\alpha = \stackrel{\frown} {SQ} = r\theta $$
Therefore, \(\tan\alpha = \theta \) and
$$ \text{inv} \alpha = \theta-\alpha = \tan\alpha-\alpha $$
parametric equations of involute curves
If the coordinates (\(x\), \(y\)) of the point \(P\) are displayed as a mediate variable,
$$ x=\rho\cos(\text{inv}\alpha) $$
$$ y=\rho\sin(\text{inv}\alpha) $$
and because the distance \(\rho\) from the origin \(O\) to the point \(P\) is represented by \(\displaystyle \rho = \frac{r}{\cos\alpha}\),
$$ x=r\frac{\cos(\text{inv}\alpha)}{\cos\alpha} = r\frac{\cos(\theta-\alpha)}{\cos\alpha}$$
$$ y=r\frac{\sin(\text{inv}\alpha)}{\cos\alpha} = r\frac{\sin(\theta-\alpha)}{\cos\alpha}$$
where, from the additive theorem for cosine and sine,
$$\cos(\theta-\alpha)=\cos\theta \cos\alpha +\sin\theta\sin\alpha$$
Since
$$ \sin(\theta-\alpha)=\sin\theta \cos\alpha-\cos\theta\sin\alpha $$
So, using \(\theta\) to display the coordinates (\(x(\theta)\), \(y(\theta)\)) of point \(P\) as the mediating variable,
$$ x(\theta)= r\frac{\cos(\theta-\alpha)}{\cos\alpha}= r(\cos\theta+\theta \cos\theta)$$
$$ y(\theta)= r\frac{\sin(\theta-\alpha)}{\cos\alpha}= r(\sin\theta-\theta\cos\theta)$$
When the radius of the base circle is 1, the involute function (text{inv}alpha) is shown below (Fig. 3) using animation in the range of ([0,\(\pi\)]) to show the involute curve.

Features of involute tooth
pressure angle
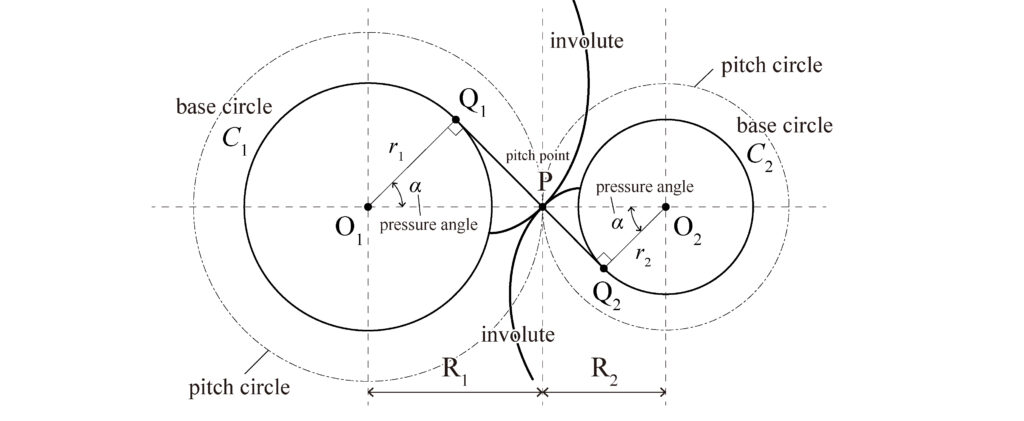
As shown in the above figure (Fig. 4), if you want to transmit rotation using an involute curve to two basic circles, the common tangent line \(Q_1, Q_2\) to the two basic circles is the common normal of the involute curve. In other words, the contact point \(P\) (pitch point) of the involute curve is always on this normal, and \(O_1P\) and \(O_2P\) are the radii \(R_1, R_2\) of the pitch circle of each gear.
The locus of the contact point is drawn on the common tangent line \(Q_1Q_2\) of the respective basic circles whose radii are \(O_1Q_1\) and \(O_2Q_2\). The angle \(\alpha\) between the locus of the contact point and the common tangent line of the pitch circle passing through point \(P\) is called the pressure angle. The pressure angle \(\alpha\) is always constant when involute tooth profiles are meshing with each other.
Generally, the standard pressure angle \(\alpha\) is \(20^\circ\).
angular velocity ratio
From Fig. 3, \(\angle Q_1O_1P=\angle Q_2O_2P=\alpha\) and
$$r_1=R_1\cos\alpha,\quad r_2=R_2\cos{\alpha}$$.
Therefore, the angular velocity ratio \(u\) is,
$$u=\frac{\omega_2}{\omega_1}=\frac{R_1}{R_2}=\frac{r_1}{r_2}$$.
It follows that The advantage of the involute tooth profile is that the angular velocity ratio does not change as long as the ratio of the radii of the basic circles remains the same even if the center distance to the pitch point \(R_1,R_2\) changes.
The speed ratio of the two gears is also given by the number of teeth \(z_1\) and \(z_2\), respectively, and the distance between adjacent teeth (circular pitch) measured on the pitch circle as \(t\),
$$ z_1=\frac{2\pi r_1}{t}, z_2=\frac{2\pi r_2}{t} $$
and \(\displaystyle \frac{r_1}{r_2}=\frac{z_1}{z_2} \), then \(\displaystyle u=\frac{z_1}{z_2}\).

コメント