歯車機構を設計する際に、常に回転を伝達する2軸が平行であり、歯車が同一平面上にある場合や、2軸が直交する場合とは限らない。
本記事では上記のような状況に限定されないようなねじれの位置の関係にある二つの歯車に対して回転を伝達させたいときを対象とした場合についてまとめる。
単双曲線回転面について
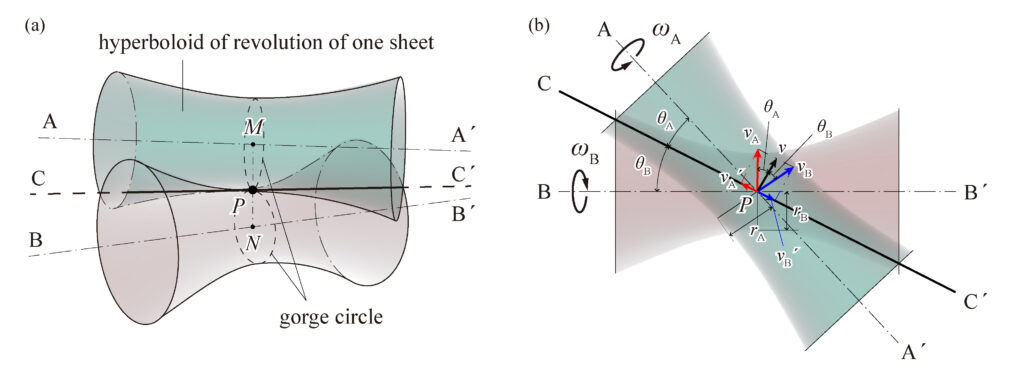
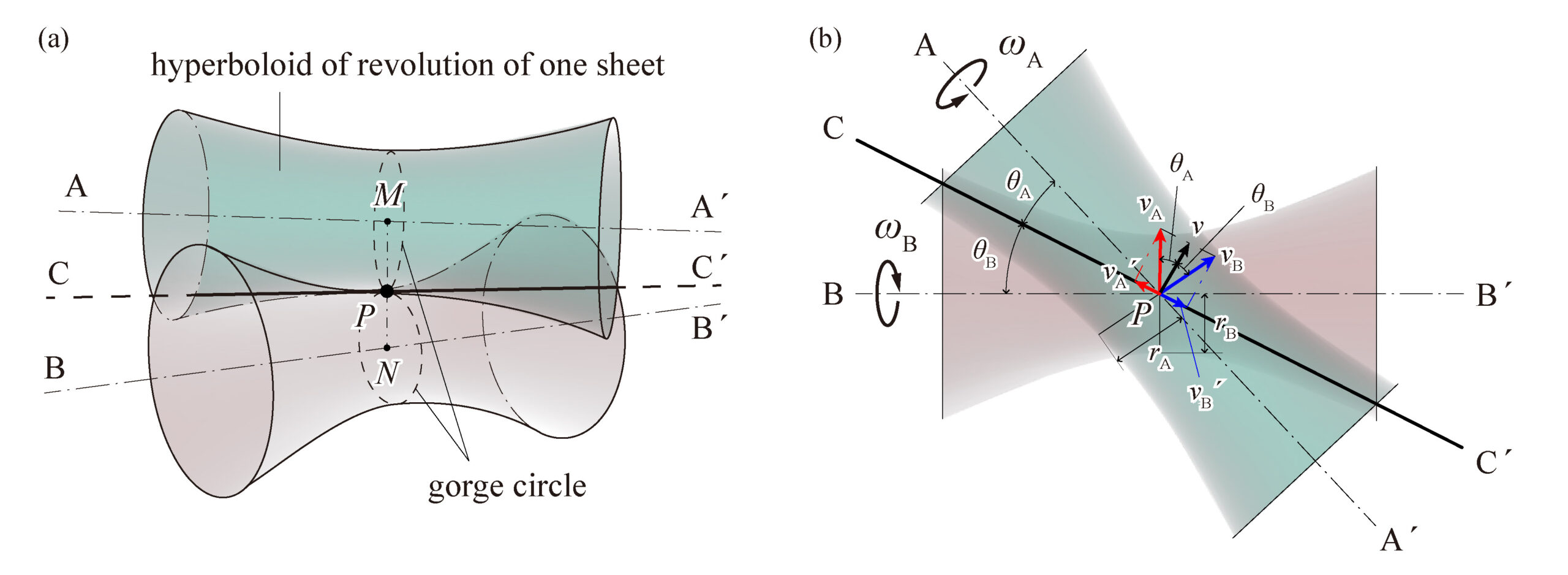
回転を伝達する2軸がねじれの位置(平行でもなく、交わりもしない場合)の接触面は単双曲線回転面(hyperboloid of revolution of one sheet)となる。
直線を母線とする線織面(ruled surface)の一つであり、ねじれの位置にある2軸に対して、一方を回転軸としてできる面である (Fig. 1 (a))。
2つの単双曲線回転面同士が接しているとき、それぞれの曲面のうち最も直径が小さい部分(曲面のくびれた部分)のことをのど円(gorge circle)と呼ぶ。のど円上の接触点Pにおけるそれぞの曲面の速度を\(v_A\)、\(v_B\)とする。また、角速度を\(\omega_A\)、\(\omega_B\)、のど円の半径を \(r_A\)、\(r_B\)とすると、\(v_A = r_A\omega_A、v_B = r_B\omega_B\) となる。
Fig. 1 (b)に示すように、この速度を接触線\(CC^\prime\)に沿う方向の速度とこれに直角方向の速度とに分解すると、転がり接触をするためには\(CC^\prime\)に直角方向の速度は等しくなければならない。\(CC^\prime\)とそれぞれの車の軸となす角を\(\theta_A\)、\(\theta_B\)とすれば
$$ v_A\cos\theta_A=v_B\cos\theta_B,\quad r_A\omega_A\cos\theta_A=r_B\omega_B\cos\theta_B$$
したがって、速度比\(u\)は、
$$ u = \frac{\omega_A}{\omega_B}=\frac{r_A\cos\theta_A}{r_B\cos\theta_B} $$
また、\(A\)軸の時間\(t\)の回転数を\(n_A\)、\(B\)軸の時間\(t\)の回転数を\(n_B\)とすると、次式の関係が得られる。
$$ v_A=\frac{\pi r_A n_A}{2t},\quad v_B=\frac{\pi r_B n_B}{2t} $$
よって、
$$ \frac{\pi r_A n_A}{2t}\cos\theta_A=\frac{\pi r_B n_B}{2t}\cos\theta_B $$
これにより、
$$ \frac{n_A}{n_B}=\frac{r_A\cos\theta_A}{r_B\cos\theta_B}=u $$
かさ歯車
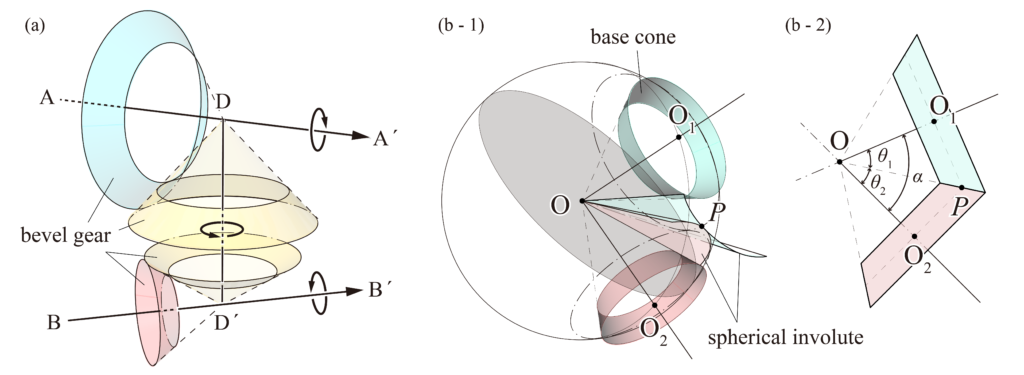
正確な製作が容易ではないことや摩擦や摩耗が大きくなることから、実用化するには困難なことが多い。そこで、2軸に交わる軸\(DD^\prime\)をつくり、これに2個の円錐車を取り付けて、各軸に設けられた円錐車と接触させて2軸間に回転運動を伝えることができる(Fig. 2 (a))。
直交する2軸間で回転を伝達するには、ピッチ面を円錐として、それに歯を付けたかさ歯車(bevel gear)を用いる。歯車の相互運動を考えるとき、歯車上の一点は2軸の交点を中心とする球面上を動くことになるため、歯形の性質を調べるためには歯形を球面曲線として扱う。インボリュート歯車では、球面インボリュート(spherical involute)となる。
上図(Fig. 2 (b-1))において、\(OO_1\)、\(OO_2\)を軸とする円錐に接する円があり、これが\(OO_1\)を軸とする円錐の側面上を転がるとき、半径\(OP\)が描く曲面が噛み合う相手の歯車の歯面となる。接触点Pの描く曲線は球面インボリュートとなっている。このときの円錐を基礎円錐(base cone)と呼び、\(O_1\)、\(O_2\)を通る円と基礎円錐に接する前述の円との交線を母線とし、それぞれ\(OO_1\)、\(OO_2\)を軸とした円錐をピッチ円錐(pitch cone)と呼ぶ。
上図(Fig. 2 (b-2))において、2軸のなす角を\(\alpha\)、各ピッチ円錐の母線と回転軸のなす角をそれぞれ\(\theta_1\)、\(\theta_2\)、歯数を\(z_1\)、\(z_2\)としたとき、以下の式が成り立つ。
$$ \tan\theta_1=\frac{\sin\alpha}{(z_2/z_1)+\cos\alpha} $$
$$ \tan\theta_2=\frac{\sin\alpha}{(z_1/z_2)+\cos\alpha} $$
つまり、\(\alpha=90^\circ\)のとき、 \(\displaystyle\tan\theta_1=\frac{z_1}{z_2}\)、\(\displaystyle\tan\theta_2=\frac{z_2}{z_1}\)となる。
また、\(\alpha=90^\circ\)かつ\(z_1=z_2\)のとき、\(\theta_1=\theta_2=45^\circ\)となる。このときの歯車をマイタ歯車(mitre gear)と呼ぶ。
食違い歯車について
製作や摩擦、摩耗による問題を考慮した上で、ねじれの位置にある2軸間に転がり接触で回転を伝える際に、単双曲線回転面の一部をピッチ曲面として母線方向に歯すじを付けた歯車を食違い歯車(skew bevel gear)と呼ぶ。
2軸が投影面状で直交する場合に用いることが多いが、軸の食い違う二つの円錐を点接触させ、ピッチ円錐として歯を刻んだものをハイポイド歯車(hypoid gear)と呼ぶ。かさ歯車と異なり、軸を双方に延長できるという利点がある。小さい方の歯車はねじ状になっており、歯の強度がかさ歯車よりも大きい。


コメント