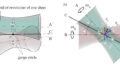
インボリュート曲線は基礎円の外側にしか定義されない。
インボリュート歯形において、接触点の軌跡は基礎円の共通接線\(EF\)が両歯車の歯先円によって挟まれた部分であるが、歯車1の歯先円が大きく歯車2のF点を超えているならば、歯車1は歯車2の歯元のインボリュートでない部分と接触することになり、正常な回転が伝えられなくなる。この現象を干渉(interference)という。このことは、相手の歯先円が基礎円の接点\(F\)または\(E\)を超すことによって起こるから、\(E\)、\(F\)を干渉点(interference point)と呼ぶ。
もし歯車1の代わりにピニオンカッタ(歯車形カッタ)を用いた場合、歯車2の歯元の邪魔となる部分が切り取られ、歯底に近いインボリュートの部分も取り去られてしまう。この現象を切下げ(undercut)という。
歯の大きさは同じでも歯車1の歯数が多いほど干渉点\(F\)を超えやすい。したがって、ラックのときが最も干渉を起こしやすい。ラック形カッタで歯車を創成するとき、歯は歯先から次第に創成され、カッタが干渉点\(F\)に達したとき、インボリュートが基礎円のところまで完全につくられる。しかし、カッタの刃先が\(F\)を超えていると、刃先の角が歯車に対して描く軌跡がトロコイドの一種であって、これが歯元をえぐり、せっかく出来上がったインボリュートの部分まで削り取ってしまい、切下げの現象が起こるのである。実際のラック形カッタの刃先の角には、破線で示したように丸みがあるが、直線刃の丸みに移る部分が干渉点を超えたときに切下げが起こる。
創生される歯車の歯数が小さいほど切下げが起きやすく、その限界の歯数は次の式で計算される。
$$ z_u=\frac{2h_k}{m\sin^2\alpha} $$
ここに、\(h_k\): 歯末のたけ、 \(m\): モジュール、 \(\alpha\): 圧力角
並歯では\(h_k=m\)となるから、
$$ z_u=\frac{2}{\sin^2\alpha} $$
となる。\(\alpha=20^\circ\)とすれば、\(z_u=17.1\)であるから、最小歯数は\(18\)である。
転位
切下げを避けるには、カッタの位置を歯車中心より遠ざけ、カッタの刃先の直線部分の端が干渉点を超さないようにすればよい。このようにカッタの位置をずらせて切削することを転位するという。カッタの位置を標準の位置から基礎円より離れる方向に移動することを正転位、基礎円の近づく方向に移動させることを負転位と呼ぶ。
これによってできた歯車は転位歯車(profile shifted gear)と呼ばれ、カッタをずらした量を転位量(amount of profile shifting)、転位量をモジュールで割った値を転位係数(shifting coefficient of profile)と呼ぶ。
転位すると、基準円や歯先円、歯元円の位置が変わる。歯厚は\(\displaystyle \frac{m}{2}\pi \)で維持する必要がある。正転位するとインボリュート曲線の曲率が大きい位置を使うことになり、根元が太く先端が細い歯形になるので、歯の曲げ強度が高まる。
歯末の幅
歯の先端の幅は転位量によって変化する。負転位の量が大きくなると、歯末の幅が減少し、\(0\)になると尖点が生じ、それ以降は尖点の位置が下がって歯末のたけが維持できない。
歯切り圧力角を\(\alpha_0\)、モジュールを\(m\)、歯数を\(z\)、転位係数を\(x\)として、次式を得る。
$$ d_b=mz\cos\alpha_0, d=m(z+2x), d_a=d+2m=m(z+2+2x) $$
インボリュート関数を考慮すると、
$$ \theta=\cos^{-1}\frac{d_b/2}{d/2}=\cos^{-1}\frac{mz\cos\alpha_0}{m(z+2x)}=\cos^{-1}\frac{z\cos\alpha_0}{(z+2x)} $$
$$ \nu=\tan\theta-\theta $$
$$ \phi=\cos^{-1}\frac{d_b/2}{d_a/2}=\cos^{-1}\frac{mz\cos\alpha_0}{m(z+2+2x)}=\cos^{-1}\frac{z\cos\alpha_0}{(z+2+2x)} $$
$$ \mu=\tan\phi-\phi $$
また、\(\gamma\)は歯厚と歯溝の幅を等しくとるため、
$$ \gamma=\frac{2\pi}{4z}=\frac{\pi}{2z} $$
歯末の幅の角度\(2\sigma\)は次式となる。
$$ 2\sigma=\gamma+\nu-\mu $$
モジュール
ピッチを\(t\)、ピッチ円の直径を\(d\)、歯数を\(z\)とすれば
$$ t=\frac{\pi d}{z} $$
となり、\(t\)の値は無理数となって、小数点以下の適当な位で止めたとしても半端な数値となる。このため\(d\)を単位\(mm\)で表したとき、
$$ m=\frac{d}{z} $$
で示した\(m\)をモジュール(module)と呼び、歯車各部の寸法を決める基準の数値とする。例えば、標準寸法の歯、すなわち並歯(full depth tooth)では、歯末のたけ\(h_k\)を\(m\)に等しくとる。また、頂げきの値は\(0.25m\)以上にするなどである。実際の歯車に用いるべき\(m\)の値は定められている。ピッチは\(t=\pi m\)で示される。互いに噛み合う一組の歯車では、ピッチは等しくならなければならないから\(m\)も等しくなければならない。
噛み合う二つの歯車のピッチ円の直径を\(d_1\)、\(d_2\)、歯数を\(z_1\)、\(z_2\)とすれば
$$ d_1=mz_1, \quad d_2=mz_2 $$
となるから、歯車の中心距離を\(a\)とすれば以下の式で表される。
$$ a = \frac{d_1}{2}+\frac{d_2}{2}=\frac{m}{2}(z_1+z_2)$$


コメント