板カム(plate cam)とは、周縁カム(peripheral cam)とも呼ばれ、ある輪郭曲線をもった板(カム)を回転させたときに、その輪郭に接しているフォロワ(follower)と呼ばれる要素(専門的な用語を用いると、カムと対偶をなす従動面)に設計者が意図した往復運動や揺動運動などの挙動を与えるものをいう。
歯車機構やカム機構を自身で設計して製作する際に意図した角速度を変化させるような複雑な挙動を与えたい場合に、カム線図というものを基にしてカムの輪郭曲線を描いていく必要がある。本記事では、カム線図についての説明から始まり、速度比の求め方について記述したのちにカムの輪郭曲線を設計する方法についてまとめる。
カム線図について
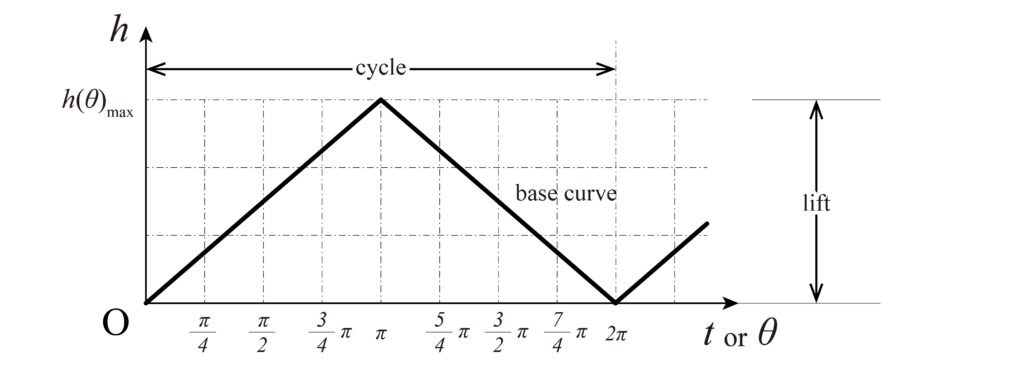
カム線図(cam chart / cam diagram)とは、カムの回転角とフォロワの変位量の関係を表した線図。上図(Fig.1)に示すように、横軸に時間またはカムの角変位をとり、縦軸にはフォロワの変位をとる。図の線を基礎曲線(base curve)、最大変位量\(h\)をリフト(lift)と呼ぶ。
運動をフォロワに与える板カムの輪郭線は、基礎円(base circle)と呼ばれる回転軸を中心に持つ基準となるある半径\(r\)の円にカム線図の基礎曲線を巻き付けることで得られる。
速度比
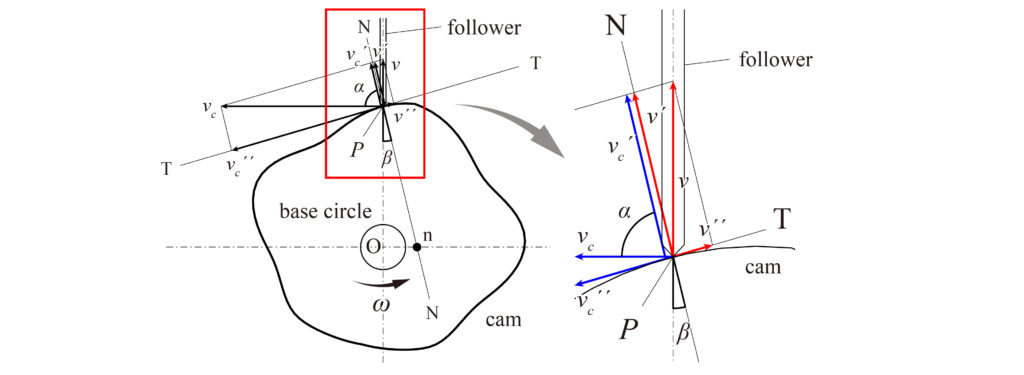
カム線図からカムの輪郭線を得る前に、速度比の求め方について整理する必要がある。ここではカムの位置は固定しフォロワのみが直線運動を例に挙げて導出する。
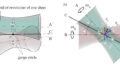
カムの角速度を\(\omega\)、フォロワの速度を\(v\)、接触点を\(P\)として、\(P\)点における共通接線\(TT\)と共通法線\(NN\)を引き、\(P\)点をカム上の一点としたときの速度\(v_c\)と\(P\)点をフォロワの一点としたときの速度\(v\)の法線方向成分の速度をそれぞれ\(v_c^\prime\)、\(v^\prime\)、接線方向成分の速度を\(v_c^{\prime\prime}\)、\(v^{\prime\prime}\)とする。
カムとフォロワが常に丁度接している状態を保つとき、\(v_c^\prime\ = v^\prime\)という条件が成立する。したがって、\(v_c\)、\(v\)が共通法線となす角を\(\alpha\)、\(\beta\)とすれば、
$$ v_c^\prime = v_c\cos\alpha=\omega\cdot \overline{OP}\cdot\cos\alpha $$
$$ v\prime =v\cos\beta=v\cos(\frac{\pi}{2}-\alpha)=v\sin\alpha$$
であるから、
$$ \omega\cdot \overline{OP}\cdot \cos\alpha = v\cdot\sin\alpha $$
ゆえに、
$$ \frac{v}{\omega}=\overline{OP}\cdot\frac{\cos\alpha}{\sin\alpha}=\overline{OP}\cdot\cot\alpha $$
\(O\)よりフォロワの進行方向に垂直に引いた線と\(NN\)との交点を\(n\)とすれば
$$ \frac{v}{\omega}=\overline{OP}\cot\alpha=\overline{On}$$
もしくは
$$v=\omega\cdot\overline{On}$$
として表される。
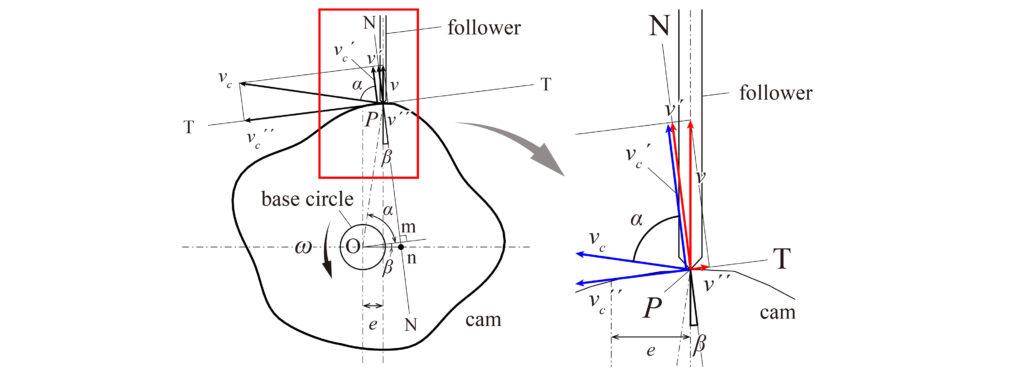
フォロワの軸線がカムの回転軸中心\(O\)を通らない場合においても考慮すると、軸線が回転軸から\(x\)軸方向にeだけ偏心しているとしたとき、上図(Fig.2)において、\(v_c^\prime=v_c\cos\alpha=\omega\cdot\overline{OP}\cdot\cos\alpha\)、\(v^\prime=v\cos\beta\)、\(v_c^\prime=v^\prime\)とすれば、
$$\omega\cdot\overline{Om}=v\cos\beta$$
\(O\)より\(NN\)に垂線を下ろし、その足を\(m\)とすると、\(\overline{OP}\cdot\cos\alpha=\overline{Om}\)であるから
$$ \omega\cdot\overline{Om}=v\cos\beta $$
したがって、
$$ \frac{v}{\omega}=\frac{\overline{Om}}{\cos\beta}=\overline{On}$$
これにより、偏心量\(e\)の違いは影響しないことがわかった。
圧力角
Fig.2やFig.3の圧力角(pressure angle)\(\beta\)は、カム機構のフォロワの軸線と接触点における共通接線とのなす角を表す。圧力角は大きくなりすぎるとカム機構の回転を妨げる要因となるため、基本的に30\(^\circ\)とする。
同じカム線図からカムの輪郭曲線を得る場合に、基礎円が小さいほど圧力角\(\beta\)は大きくなる。回転を伝達させやすくするためには、基礎円を大きくする方が望ましい。
カムの輪郭曲線
ここでは、ある運動を設定した上でカム線図を考え、最終的な輪郭曲線を求めるという手順を例を挙げながら記す。また、フォロワの軸線は常に基礎円の中心\(O\)を通るとする。
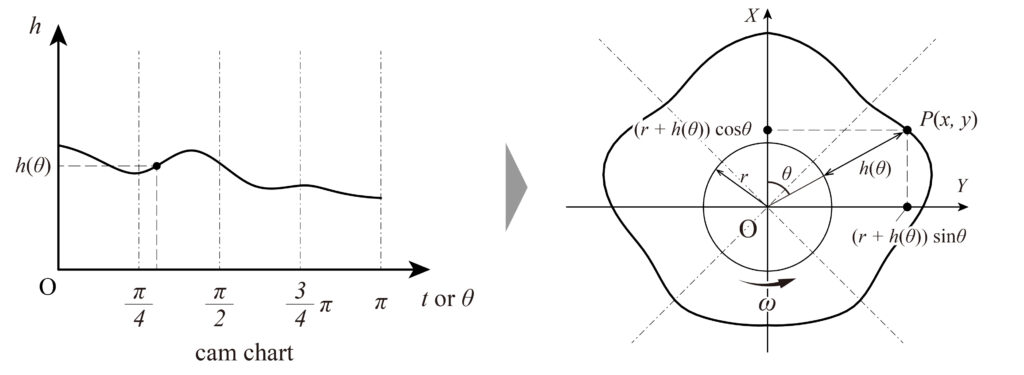
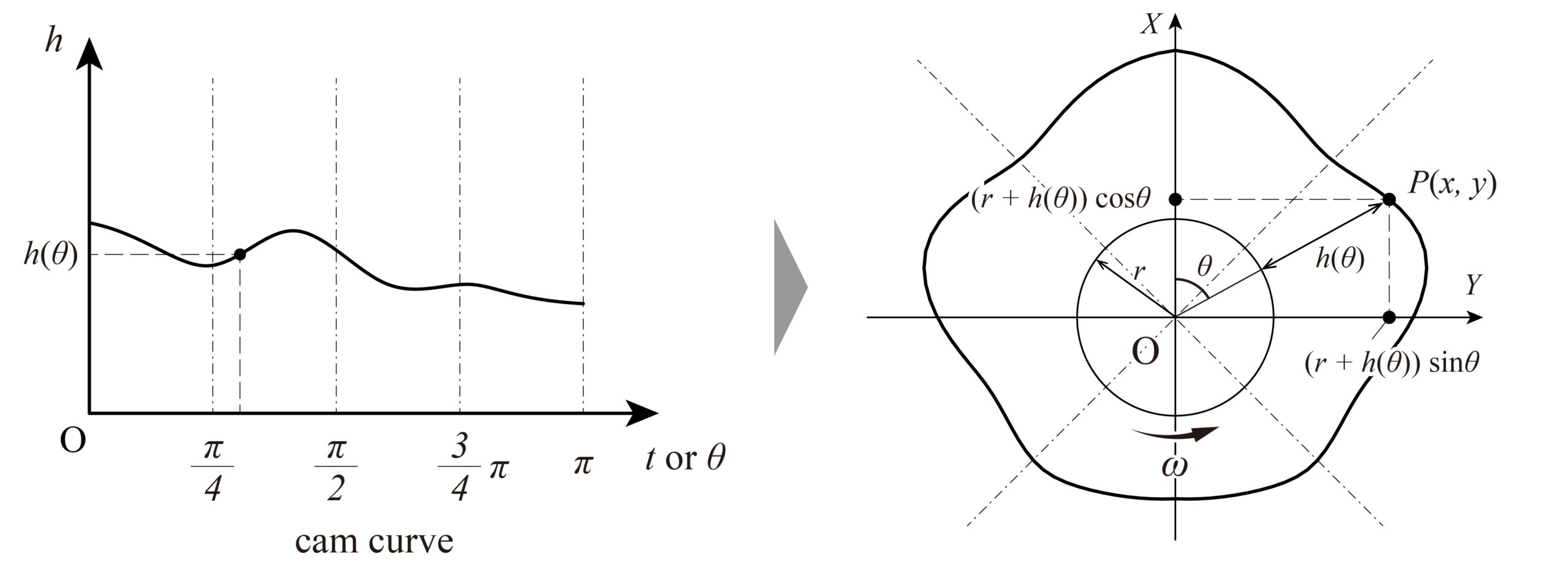
上図に示すように、カムが等角速度\(\omega\)で回転する場合、基礎円に対して[0,\(\pi\)]のカム線図があるとき、カム線図を分割して基礎円に対応する角度に対して変位分の輪郭を与える。すなわち、カム線図の直交座標系から半径\(r\)の基礎円上の極座標に変換することでカムの輪郭曲線を得る。カムの輪郭曲線上の点\(P\)(\(x\),\(y\))を媒介変数表示すると、以下の式で表せる。
$$ x = ( r + h(\theta))\sin\theta $$
$$ y = ( r + h(\theta))\cos\theta $$
フォロワの運動の例
等速度運動 (\(v=\text{const.}\)) するカム線図
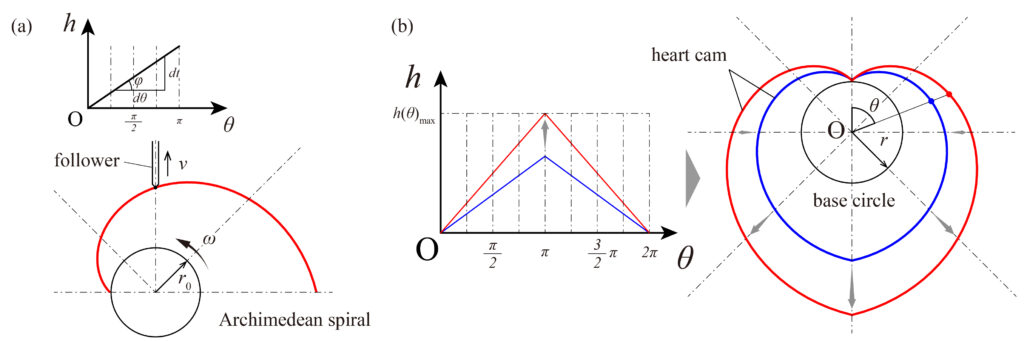
恐らくカムを自由に設計する上での要求として、速度もしくは加速度が一定ではない機構を狙って作りたいことが挙げられると想定した。しかし、その前に最も基本となる等速運動と呼ばれる速度一定の時の挙動についてのカム線図について述べる。
フォロワの変位を\(h\)、速度を\(v\)とするが、フォロワは等速運動をするため以下の式が成り立ち、カム線図は傾き\(\phi\)の直線を示す (Fig. 5 (a))。
$$ v=\frac{dh}{dt}=\tan\phi=\text{const.} $$
カムが等角速度\(\omega\)で回転し、フォロワの軸線がカムの回転軸中心\(O\)を通る場合に、カムの輪郭曲線は回転軸中心\(O\)を原点としたときの極座標 \(r=r+a\theta\) となる。ここで、\(r\)は基礎円の半径を表しており、\(\theta\)は回転開始時の軸線に対する動径のなす角とする。また、\(\displaystyle a=\frac{dh}{d\theta}\) であり、カムは等角速度で回転するため、
$$ a=\frac{dh}{d\theta}=\frac{v\cdot dt}{\omega\cdot dt}=\frac{v}{\omega}=\text{const.} $$
となる。この曲線はアルキメデスの螺旋(Archimedean spiral)とも呼ばれている。この曲線を半周期ずつ反転させてつないだ形の輪郭曲線をもつカムをハートカム(heart cam)と呼ぶ (Fig. 5 (b))。
等加速度運動 (\(a=\text{const.}\)) するカム線図
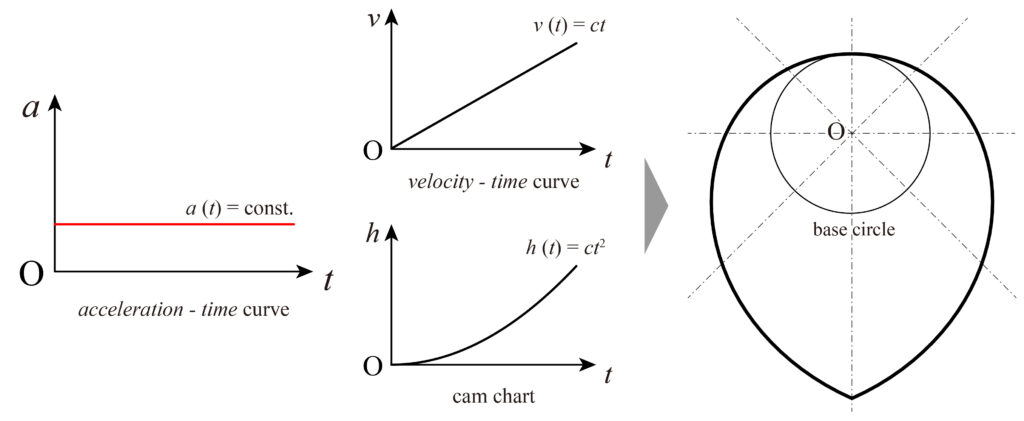
まず、等加速度運動と呼ばれる加速度は一定で、速度を段々と変化させるような挙動を実現したい場合についてである。初速度が0のとき、変位が\(h\)、加速度\(a\)、時間\(t\)と置くと、\(\displaystyle h=\frac{a}{2}t^2\)となる。
ここで、\(a\)は一定であるから定数\(c\)として\(\displaystyle c=\frac{a}{2}\)とすると、\(h=ct^2\)と表され、カム線図は放物線となることがわかる。ここで、カムの回転による角速度が一定である場合は、時間\(t\)をカムの回転角\(\theta\)と置くことも可能である。
カム線図を最大変位量(リフト)で反転させると、カム線図が連続的に繋がるため半周でフォロワは最高速となり、半周を超えると徐々に減速する運動を実現できる。このときのカムの輪郭曲線は、下図(Fig. 6)に示すような形状となる。
加速度から設定したときのカム線図
仮に加速度を上に示す加速度線図のようなある2次曲線 \(a(t)=ct^2\)で設計しようと考えたとする。\(\displaystyle a(t)=\frac{dv}{dt}\)より、\(\displaystyle v(t)=\int a(t)dt\)であるから、\(\displaystyle v(t)=\frac{1}{3}ct^3+C\)である (\(C\)は積分定数)が、\(v(0)=0\) とすると、\(\displaystyle v(t)=\frac{1}{3}ct^3\)となる。同様に、\(\displaystyle v(t)=\frac{dh}{dt}\)より、\(\displaystyle h(t)=\int v(t)dt=\frac{1}{12}ct^4+C\)であり、\(h(0)=0\) とすると、\(\displaystyle h(t)=\frac{1}{12}ct^4\)となる。
加速度から設定した場合、加速度線図よりもカム線図の次数が2つ増えるため、最終的な曲線は4次曲線となる。

コメント